线段树

线段树和树状数组一样，他储存的是原数组中某个区间的信息，但是他比树状数组更加全能，用树状数组能实现的基本上都能用线段树来实现，反之则不一定成立，但是树状数组的常数比线段树小。

只要是某个大区间的信息能够由两个更小区间的信息合并而来，那么就可以用线段树来进行处理。

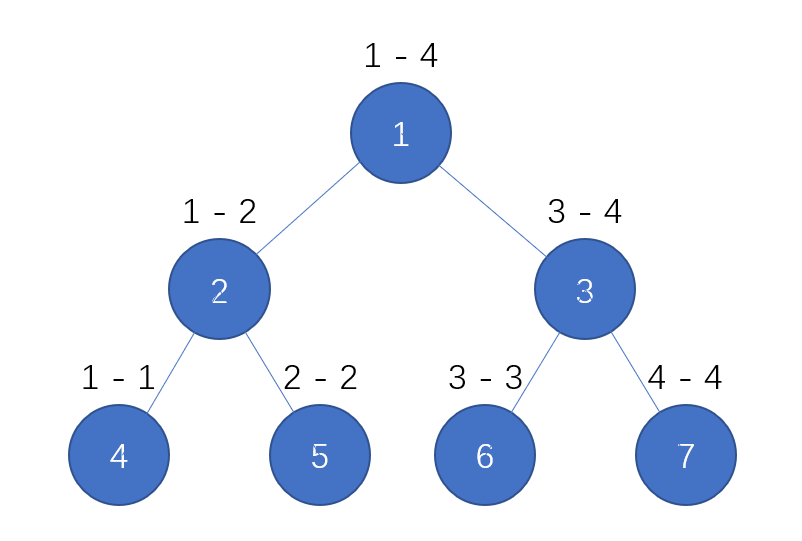
基础知识

观察上图，这就是一颗很普通的线段树，其中1号节点储存的是原数组中1-4的信息，2号存储1-2的信息，4号储存1-1的信息。如果我们想知道1-2的信息，那么我们可以由1-1 ， 2-2的信息合并而来，同理，如果我们想知道1-3的信息，那么我们可以用1-2 ， 3-3的信息合并起来。而且我们在预处理的时候就能够将1-2的信息给处理出来，这样就可以直接使用处理好的信息。

如果我们想修改某个区间的信息，例如2-2的信息，那么我们只需要修改5，2，1三个节点的数据即可。

查询的时间复杂度为O(log n) ，修改的复杂度为O(log n)。

详细知识

代码例题

对于此题，每个节点需要储存的信息为，节点左边界，右边界，区间和

const int maxn = 1e5+5;
struct node{
    int l, r;
    long long sum;
}tree[maxn * 4]; // 线段树一般开4倍空间
long long a[maxn];//原数组

开点建树

利用数组来模拟树，以p*2为左节点，p*2+1为右节点，每个节点处理一半的信息。注意当当前区间左节点与右节点相同时，代表已经到达了叶子节点，此时的信息可以从数组中直接得到。由于递归，当左右两颗树都建好了，那么左右两颗树的信息也都处理好了，此时就能够由两颗树直接处理。时间复杂度为O(nlogn) 。详细看代码。

/*
p: 当前节点编号
l: 当前节点左边界
r: 当前节点右边界
*/
void build(int p, int l, int r){
    tree[p].l = l;
    tree[p].r = r;
    if(l == r){//到了最下方的节点，此时节点直接对应数组
        tree[p].sum = a[l]; // l-l的和就是a[l]，因为只有一个节点，其他情况自由发挥
        return;
    }
    int mid = (l + r) / 2; //将当前区间分割成两个小区间
    build(p*2, l, mid);
    build(p*2+1, mid + 1, r);
    tree[p].sum = tree[p*2].sum + tree[p*2+1].sum; // 大区间的和为两个小区间的和之和c
}

查询

题目中的操作2，如果我们想知道 [l,r] 的和，那么我们直接去线段树中去寻找即可，注意区间的划分，详细看代码。

/*
p: 当前节点
l: 目标区间左端点
r: 目标区间右端点
*/
long long query(int p, int l, int r){
    if(tree[p].l >= l && tree[p].r <= r) return tree[p].sum; // 当前节点所存储的区间在目标区间之内，那么我们直接用当前节点的信息即可
    int mid = (tree[p].l + tree[p].r) / 2; // 注意是将当前区间分割成两半
    long long sum = 0;
    if(mid >= l)  sum += query(p*2, l, r); // 如果有部分目标区间在当前区间所划分的左区间之内，那么去左区间瞅瞅
    if(mid+1 <= r) sum += query(p*2+1, l, r); // 如果有部分目标区间在当前区间所划分的右区间之内，那么去右区间瞅瞅
    return sum;
}

至此，操作2已经完成，即线段树的查询已经结束。接下来是更新的内容了。

更新

先来常规更新

常规更新

与查询类似，如果要更新某个区间的值，那么我们只需要不断的去寻找这个区间，把最下面的节点更改掉，然后更新一下节点的和即可。注意此时的复杂度为O(n log n)。

/*
p: 当前节点
l: 目标区间左端点
r: 目标区间右端点
k: 增加的数
*/
int update(int p, int l, int r, long long k){
    if(tree[p].l == tree[p].r){ // 到达叶子节点
        tree[p].sum += k; // 区间增加分解到点增加
        return;
    }
    int mid = (tree[p].l + tree[p].r) / 2;
    if(mid >= l) update(p*2, l, r, k); // 如果有部分目标区间在当前区间所划分的左区间之内，那么去左区间改改
    if(mid + 1 <= r) update(p*2+1, l, r, k); // 如果有部分目标区间在当前区间所划分的右区间之内，那么去右区间改改。
    tree[p].sum = tree[p*2].sum + tree[p*2+1].sum; // 更新当前区间新的和
}

可以发现，这样看起来虽然很高级，但是也有点傻。线段树他是储存的区间信息，那么我们可不可以先把区间处理了，小区间先放一放，等后面要用小区间的信息了再去处理，这样是不是会快一些。此时，我们引入 懒标记 。

懒标记

懒标记是对区间是否应该修改进行标记。是否应该修改，应该怎么修改，应该修改多少等等等等，这些都能用懒标记来进行懒处理。

懒标记主要体现在一个懒字，正如上文所说，我们可以先不处理小区间的信息，先处理大区间的信息，把小区间需要处理标记一下，等下次要用这个小区间了，再来处理这个小区间。说起来有点抽象，下面用代码来解释。

long long mark[maxn * 4]; // 懒标记是对线段树节点进行懒标记
void pushdown(int p){
    if(mark[p] != 0){ // 如果存在懒标记
        int l = tree[p].l, r = tree[p].r;
        int mid = (l + r) / 2;
        mark[p*2] += mark[p]; // 懒标记往下传
        mark[p*2+1] += mark[p];
        tree[p*2].sum += (mid - l + 1) * mark[p]; // 区间增加相同的数，即区间和增加 数字*数量
        tree[p*2+1].sum += (r - (mid+1) + 1) * mark[p];
        mark[p] = 0; // 清楚当前节点的懒标记
    }
}
int update(int p, int l, int r, long long k){
    if(tree[p].l >= l && tree[p].r <= r){
        tree[p].sum += (tree[p].r - tree[p].l + 1) * k;
        mark[p] += k;
        return;
    }
    pushdown(p);// 把当前节点的懒标记传下去
    int mid = (tree[p].l + tree[p].r) / 2;
    if(mid >= l) update(p*2, l, r, k);
    if(mid + 1 <= r) update(p*2+1, l, r, k);
    tree[p].sum = tree[p*2].sum + tree[p*2+1].sum;
}
long long query(int p, int l, int r){
    if(tree[p].l >= l && tree[p].r <= r) return tree[p].sum;
    pushdown(p); // 注意懒标记
    int mid = (tree[p].l + tree[p].r) / 2;
    long long sum = 0;
    if(mid >= l)  sum += query(p*2, l, r);
    if(mid+1 <= r) sum += query(p*2+1, l, r);
    return sum;
}

注意建树，修改，查询时，都是从最大的节点，即1号节点开始走。

例题完整代码

下面给出题目完整代码

#include<iostream>
using namespace std;
const int maxn = 1e5+5;
struct node{
    int l, r;
    long long sum;
}tree[maxn * 4]; // 线段树一般开4倍空间
long long a[maxn], mark[maxn * 4];
void build(int p, int l, int r){
    tree[p].l = l;
    tree[p].r = r;
    if(l == r){//到了最下方的节点，此时节点直接对应数组
        tree[p].sum = a[l]; // l-l的和就是a[l]，因为只有一个节点，其他情况自由发挥
        return;
    }
    int mid = (l + r) / 2; //将当前区间分割成两个小区间
    build(p*2, l, mid);
    build(p*2+1, mid + 1, r);
    tree[p].sum = tree[p*2].sum + tree[p*2+1].sum; // 大区间的和为两个小区间的和之和c
}
void pushdown(int p){
    if(mark[p] != 0){ // 如果存在懒标记
        int l = tree[p].l, r = tree[p].r;
        int mid = (l + r) / 2;
        mark[p*2] += mark[p]; // 懒标记往下传
        mark[p*2+1] += mark[p];
        tree[p*2].sum += (mid - l + 1) * mark[p]; // 区间增加相同的数，即区间和增加 数字*数量
        tree[p*2+1].sum += (r - (mid+1) + 1) * mark[p];
        mark[p] = 0; // 清楚当前节点的懒标记
    }
}
void update(int p, int l, int r, long long k){
    if(tree[p].l >= l && tree[p].r <= r){
        tree[p].sum += (tree[p].r - tree[p].l + 1) * k;
        mark[p] += k;
        return;
    }
    pushdown(p);// 把当前节点的懒标记传下去
    int mid = (tree[p].l + tree[p].r) / 2;
    if(mid >= l) update(p*2, l, r, k);
    if(mid + 1 <= r) update(p*2+1, l, r, k);
    tree[p].sum = tree[p*2].sum + tree[p*2+1].sum;
}
long long query(int p, int l, int r){
    if(tree[p].l >= l && tree[p].r <= r) return tree[p].sum;
    pushdown(p); // 注意懒标记
    int mid = (tree[p].l + tree[p].r) / 2;
    long long sum = 0;
    if(mid >= l)  sum += query(p*2, l, r);
    if(mid+1 <= r) sum += query(p*2+1, l, r);
    return sum;
}
int main(void){
    int n, m;
    cin>>n>>m;
    for(int i = 1;i <= n;i++) cin>>a[i];
    build(1, 1, n);
    for(int i = 0;i < m;i++){
        int ch;
        cin>>ch;
        if(ch == 2){
            int l, r;
            cin>>l>>r;
            cout<<query(1, l, r)<<endl;
        }else{
            int l, r, k;
            cin>>l>>r>>k;
            update(1, l, r, k);
        }
    }
    return 0;
}

---

上文为crotes编写，下文为currywoe编写

线段树进阶技巧

约 3545 个字 735 行代码 预计阅读时间 21 分钟

下文需要读者熟悉最朴素的单点修改区间查询，维护区间信息的线段树作为基础，例程如下：

typedef long long ll;
const int N=1e5+3;
ll a[N];//a为初始序列,有n个元素，1-indexed
struct SegmentTree
{
    struct node
    {
        ll sum;
    }st[N<<2];
    void build(int id,int l,int r)
    {
        if (l ==r)
        {
            st[id]={a[l]};
            return;
        }
        int mid=(l + r)/2;
        build(id << 1,l,mid);
        build(id<<1|1,mid + 1,r);
        st[id].sum=st[id<<1].sum+st[id<<1|1].sum;
    }
    void update(int id,int segl,int segr,int pos,ll val)
    {
        if (segl==segr)
        {
            st[id].sum+=val;
            return;
        }
        int mid=(segl + segr)/2;
        if (pos<=mid)
            update(id << 1,segl,mid,pos,val);
        else
            update(id<<1|1,mid+1,segr,pos,val);
        st[id].sum=st[id<<1].sum+st[id<<1|1].sum;
    }
    ll query(int id,int segl,int segr,int L,int R)
    {
        if (L <=segl && segr <=R)
            return st[id].sum;
        int mid=(segl + segr)/2;
        ll res=0;
        if (L <=mid)
            res+=query(id << 1,segl,mid,L,R);
        if (R > mid)
            res+=query(id<<1|1,mid+1,segr,L,R);
        return res;
    }
}st;
st.build(1,1,n);
st.update(1,1,n,pos,val);
st.query(1,1,n,l,r);

一些零碎细节

array of struct 比 struct of array 略快一点

实时计算点的l，r，比存下来去找，快

求mid用右移比除2，快。因为编译器不会把有符号除2的幂优化为右移

segl是负数时只能用右移，因为-3/2=-1，偏右

当值域特别大的时候(segl+segr)会溢出，正确写法是(segl>>1)+(segr>>1)+(segl&segr&1)

懒标记(lazy tag)

当试图修改 $[l,r]$ 区间的元素，如果采用最朴素版本的修改，每次操作的复杂度是 $O((r-l+1)\log n)$，当操作次数很多，时间复杂度就爆炸

线段树上节点sum表示的意义，是一段区间的信息，而修改也是一种区间的信息。那么可以把修改信息放在一个节点上，表示这个区间都要受到这种修改。

朴素版每次修改后，每个节点的sum真的表示一段区间的信息。因为朴素版修改了所有受到影响的节点

懒标记只修改了部分收到影响的节点，因此称为懒标记。因此sum的意义也变了，表示一段时间之前，这段区间的信息

实现

每个节点加上变量lazy tag表示懒标记，修改或查询的递归之前都下推懒标记(pushDown)，来保证左右儿子区间的信息是最新的

修改：如果一个节点的区间都要被修改，那就把修改信息放在这里，不再搜索到叶子节点；否则继续向下递归

查询：和朴素版类似，多了下推懒标记

在建树和修改，都需要合并左右儿子信息，为了复用这段代码，有pushup函数

struct SegmentTree
{
    struct node
    {
        ll sum,lz;
    }st[N<<2];
    void pushup(int id)
    {
        st[id].sum=(st[id<<1].sum+st[id<<1|1].sum);
    }
    void pushdown(int id,int lsonlen,int rsonlen)
    {
        if (!st[id].lz)
            return;
        st[id<<1].lz+=st[id].lz;
        st[id<<1|1].lz+=st[id].lz;
        st[id<<1].sum+=st[id].lz*lsonlen;
        st[id<<1|1].sum+=st[id].lz*rsonlen;
        st[id].lz=0;
    }
    void build(int id,int l,int r)
    {
        if (l ==r)
        {
            st[id]={a[l],0};
            return;
        }
        int mid=(l + r)/2;
        build(id << 1,l,mid);
        build(id<<1|1,mid + 1,r);
        pushup(id);
    }
    void update(int id,int segl,int segr,int l,int r,ll val)
    {
        if (l <=segl && segr <=r)
        {
            st[id].sum+=val*(segr-segl+1);
            st[id].lz+=val;
            return;
        }
        int mid=(segl + segr)/2;
        pushdown(id,mid-segl+1,segr-mid);
        if (l <=mid)
            update(id << 1,segl,mid,l,r,val);
        if (r > mid)
            update(id<<1|1,mid+1,segr,l,r,val);
        pushup(id);
    }
    ll query(int id,int segl,int segr,int l,int r)
    {
        if (l <=segl && segr <=r)
            return st[id].sum;
        int mid=(segl + segr)/2;
        pushdown(id,mid-segl+1,segr-mid);
        ll res=0;
        if (l <=mid)
            res+=query(id << 1,segl,mid,l,r);
        if (r > mid)
            res+=query(id<<1|1,mid+1,segr,l,r);
        return res;
    }
}st;
st.build(1,1,n);
st.update(1,1,n,l,r,val);
st.query(1,1,n,l,r);

注意

如果混用单点修改和区间修改，单点修改时也需要下推标记

标记永久化

思想类似懒标记，修改信息放在一个节点上，表示这个区间都要受到这种修改。

不同于懒标记：不下推标记；修改时直接加上影响；查询时带上标记

实现

struct SegmentTree
{
    struct node
    {
        ll sum,lz;
    }st[N<<2];
    void build(int id,int l,int r)
    {
        if (l ==r)
        {
            st[id]={a[l],0};
            return;
        }
        int mid=(l + r)/2;
        build(id << 1,l,mid);
        build(id<<1|1,mid + 1,r);
        st[id].sum=(st[id<<1].sum+st[id<<1|1].sum);
    }
    void update(int id,int segl,int segr,int l,int r,ll val)
    {
        if (l <=segl && segr <=r)
        {
            st[id].sum+=val*(segr-segl+1);
            st[id].lz+=val;
            return;
        }
        int mid=(segl + segr)/2;
        if (l <=mid)
            update(id << 1,segl,mid,l,r,val);
        if (r > mid)
            update(id<<1|1,mid+1,segr,l,r,val);
        st[id].sum+=val*(min(segr,r)-max(segl,l)+1);
    }
    ll query(int id,int segl,int segr,int l,int r,ll lz)
    {
        if (l <=segl && segr <=r)
            return st[id].sum+lz*(segr-segl+1);
        int mid=(segl + segr)/2;
        ll res=0;
        if (l <=mid)
            res+=query(id << 1,segl,mid,l,r,lz+st[id].lz);
        if (r > mid)
            res+=query(id<<1|1,mid+1,segr,l,r,lz+st[id].lz);
        return res;
    }
}st;
st.build(1,1,n);
st.update(1,1,n,l,r,val);
st.query(1,1,n,l,r,0ll);

懒标记和标记永久化的对比

平衡树这样点的相对位置会改变的，只能用懒标记，保证碰到的节点，其信息是最新的。

可持久化这样一个点有多个父亲的，如果用懒标记，下传标记如果不开新节点会影响前面的树，开新节点容易卡空间，只能用标记永久化。

其他情况用两个都行。

静态开点

定义：所有要表示的区间，其节点下标已经确定

朴素版就是一种静态开点，根节点为1，假设当前节点id，左右儿子分别是 $id*2$ 和 $id*2+1$。这种方式用到的节点数小于2n，用到的最大下标小于4n。

另一种静态开点，可以使用到的最大下标小于2n，但是常数略差，猜测是访存不够连续，cache经常miss，根据洛谷模板题“线段树3”的测试，大约慢了36%。做法就是当前点的左右儿子是 $mid*2$ 和 $mid*2+1$

第二种静态开点的证明见帖子第二页

动态开点

定义：所有要表示的区间，实时分配其节点下标

每个节点新增两个变量l，r，表示其左右儿子的节点下标

不使用0作为实际存在的节点的下标，且信息(sum)为空。若某节点的下标为0，表示尚未分配下标

修改时搜索到尚未分配下标的节点，直接分配一个新的下标

查询时搜索到尚未分配下标的节点，说明没有信息要合并，直接返回

初始化要把所有节点都设置为尚未分配下标

namespace SegmentTree
{
    struct node
    {
        int l,r;
        ll sum;
    }st[N];
    int tot;
    void update(int &id,int segl,int segr,int pos, ll val)
    {
        if(!id)
            id=++tot;
        if (segl==segr)
        {
            st[id].sum+=val;
            return;
        }
        int mid = (segl + segr)/2;
        if (pos <= mid)
            update(st[id].l,segl,mid,pos,val);
        else
            update(st[id].r,mid+1,segr,pos,val);
        st[id].sum=st[st[id].l].sum+st[st[id].r].sum;
    }
    ll query(int id,int segl,int segr,int L, int R)
    {
        if(!id)
            return 0;
        if (L <= segl && segr <= R)
            return st[id].sum;
        int mid = (segl + segr)/2;
        ll res = 0;
        if (L <= mid)
            res+=query(st[id].l, segl,mid,L, R);
        if (R > mid)
            res+=query(st[id].r,mid+1,segr, L, R);
        return res;
    }
    void init()
    {
        for(;tot;--tot)
            st[tot]={0,0,0ll};
    }
};
st::init();
st::update(1,1,n,pos,x);
st::query(1,1,n,l,r);

加内存池的动态开点

如果认为一个节点暂时无用，回收该节点的下标，在申请下标时优先使用回收的下标

对于信息是区间和的情况，当节点信息为0时，认为其暂时无用

部分毒瘤题需要此技巧，省空间

namespace segmentTreeWithMemoryPool
{
    struct node
    {
        int l,r;
        ll sum;
    }st[N];
    int tot;
    vector<int> memoryPool;
    void newNode(int &id)
    {
        if(memoryPool.empty())
            id=++tot;
        else
        {
            id=memoryPool.back();
            memoryPool.pop_back();
        }
    }
    void delNode(int &id)
    {
        memoryPool.push_back(id);
        id=0;
    }
    void update(int &id, int l, int r,int pos,ll val)
    {
        if(!id)
            newNode(id);
        st[id].sum+=val;
        if(l==r)
            return;
        int mid = (l+r)/2;
        if (pos <= mid)
            update(st[id].l,l,mid,pos,val);
        else
            update(st[id].r,mid+1,r,pos,val);
        if(st[id].sum==0)
            delNode(id);
    }
    ll query(int id,int segl,int segr,int l, int r)
    {
        if(!id)
            return 0;
        if (l <= segl && segr <= r)
            return st[id].sum;
        int mid = (segl + segr)/2;
        ll res=0;
        if (l <= mid)
            res+=query(st[id].l,segl,mid,l,r);
        if (r > mid)
            res+=query(st[id].r,mid+1,segr,l,r);
        return res;
    }
};

静态开点和动态开点的对比

静态开点：占用空间大，时间快

动态开点：占用空间小，时间慢。

静态开点4n就行，动态开点需要手算一下空间，能开多大开多大，cf915E离MLE就差一点才能AC。

如果需要很多颗线段树，只能用动态开点，记录下每棵树根分配到的下标

要表示的区间很多而有用的区间少，只能用动态开点。

权值线段树

朴素版是维护区间信息的，权值线段树是维护值域内数的个数

$[2,3,1,2,2,3]$ 这个原序列，转化为值域序列就是 $[1,3,2]$ ，表示1的个数有1个，2的个数有3个，3的个数有2个

权值线段树的操作和朴素版几乎一致，只是维护信息不同。

通常题目的值域会很大，可以通过离散化或者动态开点解决

01字典树和强制值域为 $[0,2^k]$ 的动态开点权值线段树，获得的树形结构是一模一样的，但是由于写法不同，01字典树常数小一点，根据luoguP1908 逆序对，约快 8%，提交1，提交2，如果01字典树要处理负值域，可以偏移，但是感觉有点屎了

下面给出动态开点，单点修改，权值线段树的例程

struct SegmentTree
{
    struct node
    {
        int l,r,sum;
    }st[N];
    int tot;
    void update(int &id, int l, int r,int val)
    {
        if(!id)
            id=++tot;
        ++st[id].sum;
        if(l==r)
            return;
        int mid = (l+r)/2;
        if (val <= mid)
            update(st[id].l,l,mid,val);
        else
            update(st[id].r,mid+1,r,val);
    }
    int query(int id,int segl,int segr,int l, int r)
    {
        if (l <= segl && segr <= r)
            return st[id].sum;
        int mid = (segl + segr)/2,res=0;
        if (l <= mid)
            res+=query(st[id].l,segl,mid,l,r);
        if (r > mid)
            res+=query(st[id].r,mid+1,segr,l,r);
        return res;
    }
    void init()
    {
        for(;tot;--tot)
            st[tot]={0,0,0};
    }
}st;
st.init();
st.update(1,MinVal,MaxVal,val);
st.query(1,MinVal,MaxVal,l,r);

线段树上二分

注意到线段树是一颗二叉树，如果信息满足二分性，那么线段树天然适合二分

这里以求全局第k小为例，如果不使用排序，可以用权值线段树+线段树上二分解决

至于为什么不使用排序，因为这个技巧是区间第k小的前置知识，直接学区间第k小，难度跨度有点大

而且不止这种信息可以用线段树上二分，例题

---

设当前节点表示值域 $[l,r]$，想求这个值域的第k小

设该节点左儿子表示值域 $[l,mid]$ ，左儿子的值域内的数有x个，若x小于k，那说明答案在右儿子的值域内，否则在左儿子的值域内

每次递归把答案所在值域缩小一半，完全符合二分

struct SegmentTree
{
    struct node
    {
        int l,r,sum;//这里的l，r表示左右儿子分配到的下标
    }st[N<<2];
    int tot;
    //初始化之后把原序列所有值扔到线段树上
    void update(int &id, int l, int r,int val)
    {
        if(!id)
            id=++tot;
        ++st[id].sum;
        if(l==r)
            return;
        int mid = (l+r)/2;
        if (val <= mid)
            update(st[id].l,l,mid,val);
        else
            update(st[id].r,mid+1,r,val);
    }
    int query(int id,int segl,int segr,int k)
    {
        if (segl==segr)
            return segl;
        int mid = (segl + segr)/2;
        if (st[st[id].l].sum>=k)
            return query(st[id].l,segl,mid,k);
        return query(st[id].r,mid+1,segr,k);
    }
    void init()
    {
        for(;tot;--tot)
            st[tot]={0,0,0};
    }
}st;
st.init();
for(int i=1;i<=n;++i)
    st.update(1,MinVal,MaxVal,a[i]);
st.query(1,MinVal,MaxVal,k);

可持久化(persistent)

笔者感觉这个翻译不够好，但是大家都是这么叫的

定义：初始有一个信息为空的东西，不断对其修改，会产生多个版本，保存每个历史版本就是可持久化

比如photoshop上画画，可以撤销上一次画的东西，也就是回到上一个版本

应用到线段树上，最朴素的方法是，每次修改都新建一颗树，继承上一棵树的信息，同时把这一次修改的信息添加上

但是很明显时空复杂度都不可接受。注意到每次修改只有部分点受到影响，因此可以共用没受到影响的点

struct persistentSegmentTree
{
    int tot,n,rtnum;//rtnum表示版本数量
    int rt[N];//每棵树根分配到的下标
    struct node
    {
        int l,r;
        ll sum;
    }st[N<<5];
    void build(int &id,int l,int r)
    {
        id=++tot;
        if(l==r)
        {
            st[id].sum=a[l];
            return;
        }
        int mid=(l+r)/2;
        build(st[id].l,l,mid);
        build(st[id].r,mid+1,r);
        st[id].sum=st[st[id].l].sum+st[st[id].r].sum;
    }
    //单点修改
    void update(int &id,int pre,int l,int r,int pos,ll val)
    {
        id=++tot;
        st[id]=st[pre];//继承上一棵树表示相同区间的对应节点的信息
        st[id].sum+=val;
        if(l==r)
            return;
        int mid=(l+r)/2;
        if(pos<=mid)
            update(st[id].l,st[id].l,l,mid,pos,val);
        else
            update(st[id].r,st[id].r,mid+1,r,pos,val);
    }
    ll query(int id,int segl,int segr,int l,int r)
    {
        if(!id)
            return 0;
        if(l<=segl && segr<=r)
            return st[id].sum;
        int mid=(segl+segr)/2;
        ll res=0;
        if(l<=mid)
            res+=query(st[id].l,segl,mid,l,r);
        if(r>mid)
            res+=query(st[id].r,mid+1,segr,l,r);
        return res;
    }
    void update(int root,int pos,ll val)//指定版本的单点修改
    {
        update(rt[++rtnum],rt[root],1,n,pos,val);
    }
    ll query(int root,int l,int r)//指定版本的区间查询
    {
        return query(rt[root],1,n,l,r);
    }
    void init(int n)
    {
        tot=rtnum=0;
        this->n=n;
        build(rt[0],1,n);
    }
}pst;
pst.init(n);
pst.update(rt,pos,val);
pst.query(rt,l,r);

注意

求节点u为根的子树内节点v的信息合并，且uv深度差要在 $[l,r]$ 范围内，可以按照深度为版本号，dfs序作为下标，插入可持久化线段树。画图理解就是矩形和三角形面积取交得到梯形

主席树(可持久化权值线段树+线段树上二分)

区间第k小，可以转化为两个版本相减之后，第k小。版本相减类似于前缀和吧（

struct persistentWeightSegmentTree
{
    int tot,q;
    int rt[N];
    struct node
    {
        int l,r,sum;
    }st[N<<5];
    void init(int n)//原数组a（1-indexed），离散化数组C
    {
        tot=0;
        memcpy(C+1,a+1,sizeof(a[0])*(n));
        sort(C+1,C+n+1);
        q=unique(C+1,C+n+1)-C-1;
        for(int i=1;i<=n;++i)
            modify(rt[i],rt[i-1],1,q,lower_bound(C+1,C+q+1,a[i])-C);
    }
    void modify(int &id,int pre,int l,int r,int pos)
    {
        id=++tot;
        st[id]=st[pre];
        ++st[id].sum;
        if(l==r)
            return;
        int mid=(l+r)/2;
        if(pos<=mid)
            modify(st[id].l,st[id].l,l,mid,pos);
        else
            modify(st[id].r,st[id].r,mid+1,r,pos);
    }
    int query(int u,int v,int l,int r,int k)//查询区间[u,v]的第k小值的下标
    {
        if(l==r)
            return l;
        int mid=(l+r)/2,x=st[st[v].l].sum-st[st[u].l].sum;
        if(x>=k)
            return query(st[u].l,st[v].l,l,mid,k);
        return query(st[u].r,st[v].r,mid+1,r,k-x);
    }
    int ask(int l,int r,int k)
    {
        return C[query(rt[l-1],rt[r],1,q,k)];
    }
}wt;
wt.init(n);
wt.ask(l,r,k);

扫描线

离线算法，枚举一维，修改查询另一维

以求平面矩形面积的并为例

使用一条垂直于X轴的直线，从左到右来扫描这个图形

明显，只有在碰到矩形的左边界或者右边界的时候，这个线段所扫描到的情况才会改变

所以把所有矩形的入边，出边按X值排序。然后根据X值从小到大去处理，就可以用线段树来维护y方向上哪些点被矩形覆盖了

扫描线扫描到的情况变化时，对图像切一刀，那么原图像就变成多个互不重叠矩形，相邻两个边差值表示宽，y方向上被覆盖长度表示高，高宽相乘得矩形面积

例程是 hdu1542

#include<bits/stdc++.h>
using namespace std;
const int N=2e2+3;
const int M=1e5+3;
struct Line
{
    double x,y1,y2;
    int flag;
    bool operator<(const Line& o)const
    {
        return x<o.x;
    }
}a[N];
double discreY[N];
namespace segmentTree
{
    struct node
    {
        int lz;
        double sum;
    } st[M];
    void pushup(int id,int segl,int segr)
    {
        if(st[id].lz)
            st[id].sum=discreY[segr]-discreY[segl];
        else
            st[id].sum=st[id<<1].sum+st[id<<1|1].sum;
    }
    void build(int id,int l,int r)
    {
        st[id]={0,0};
        if(r-l<=1)
            return;
        int mid=(l+r)/2;
        build(id*2,l,mid);
        build(id*2+1,mid,r);
    }
    void upd(int id,int segl,int segr,int l,int r,int val)
    {
        if(l<=segl && segr<=r)
        {
            st[id].lz+=val;
            pushup(id,segl,segr);
            return;
        }
        int mid=(segl+segr)/2;
        if(l<mid)
            upd(id<<1,segl,mid,l,r,val);
        if(r>mid)
            upd(id<<1|1,mid,segr,l,r,val);
        pushup(id,segl,segr);
    }
};
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int n;
    for(int kase=1;;++kase)
    {
        cin>>n;
        if(!n)
            break;
        for(int i=1;i<=n;++i)
        {
            double x1,y1,x2,y2;
            cin>>x1>>y1>>x2>>y2;
            a[i]={x1,y1,y2,1};
            a[i+n]={x2,y1,y2,-1};
            discreY[i]=y1;
            discreY[i+n]=y2;
        }
        sort(a+1,a+n*2+1);
        sort(discreY+1,discreY+n*2+1);
        int q=unique(discreY+1,discreY+n*2+1)-discreY-1;
        double ans=0;
        segmentTree::build(1,1,q);
        for(int i=1;i<=n*2;++i)
        {
            ans+=segmentTree::st[1].sum*(double)(a[i].x-a[i-1].x);
            int y1=lower_bound(discreY+1,discreY+q+1,a[i].y1)-discreY;
            int y2=lower_bound(discreY+1,discreY+q+1,a[i].y2)-discreY;
            segmentTree::upd(1,1,q,y1,y2,a[i].flag);
        }
        cout<<"Test case #"<<kase<<"\nTotal explored area: "<<fixed<<setprecision(2)<<ans<<"\n\n";
    }
    return 0;
}

势能线段树

懒标记可以节省开销的前提是：节点的区间信息可以根据懒标记来更新；懒标记之间可以快速相互合并

但是有些区间修改操作不能依靠懒标记完成，比如区间开根号，区间位运算，因为这些运算都是依赖于叶子节点的值

以区间开根为例，1再开根还是1，所以修改没有意义，就是操作已经“退化”了

因此可以暴力开根每个叶子节点。当区间最大值都是1，说明这个区间不用递归进去修改，反正值不会变

而一个数不断开根，变成1需要的次数非常少。所以总操作次数可以保证不会太大

而势能线段树就是每个节点维护一个势能标记，就好像你一开始位于高空，每次修改会让你的高度下降，当你落到地面时，再对你修改就已经没有意义了。就是这个操作对你而言已经"退化"了。

对于区间开根，区间最大值就是势能标记。对于区间取模，区间最大值就是势能标记。对于区间变成其因子数，区间最大值就是势能标记

简而言之，势能线段树就是暴力剪枝

---

以下笔者还没学

李超线段树

线段树合并

新建式

int merge(int u, int v, int l, int r) {
    if (!u || !v)
        return u + v; // 如果有一个为空，就返回不为空的；如果都为空就返回空
    int c = ++cnt;
    if (l == r)
    {
        T[c].v = T[u].v + T[v].v;
        return c;
    }
    int mid = l + r >> 1;
    T[c].ls = merge(T[u].ls, T[v].ls, l, mid);
    T[c].rs = merge(T[u].rs, T[v].rs, mid + 1, r);
    pushup(c);
    return c;
}

挂靠式

int merge(int u, int v, int l, int r) {
    if (!u || !v)
        return u + v;
    if (l == r)
    {
        T[u].v += T[v].v;
        return u;
    }
    int mid = l + r >> 1;
    T[u].ls = merge(T[u].ls, T[v].ls, l, mid);
    T[u].rs = merge(T[u].rs, T[v].rs, mid + 1, r);
    pushup(u);
    return u;
}

线段树分裂