树状数组

约 1271 个字 150 行代码 预计阅读时间 6 分钟

基础知识

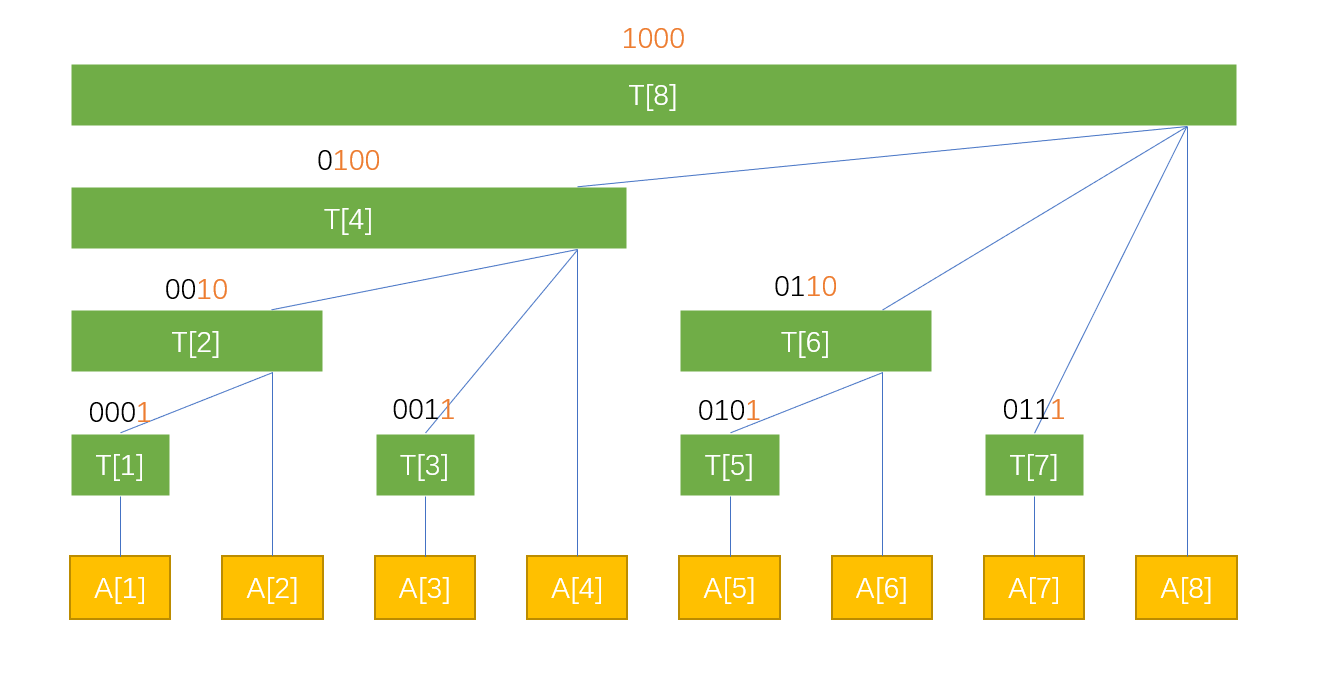
树状数组中的节点储存的是一定范围之内的和，其中节点范围可以参考下面这个图片。绿色为树状数组的节点，黄色为数组的节点。

在使用平常方法时，如果需要频繁查询某个区间的和，那么一般情况下是直接循环累加或者使用前缀和。但是如果数字可以修改呢，例如数字的修改，新增，此时不仅仅要修改数字，还要修改前缀和数组，此时复杂度为O(n)。但是如果利用树状数组，那么我们就不需要全部修改后面所有的数组，只需要修改部分就可以了，树状数组修改的复杂度为 O(log n) 。

详细知识

树状数组储存的区间范围为以当前下标开始，向左推移**最后一个1与后面所有的0**所有的范围。

用一个例子来解释：

比如上面树状数组的节点T[6] ，6转化为2进制为(0110) ，那么 最后一个1与后面所有的0 为(10)转化为10进制为2，那么T[6]所储存的便是A[6]与A[5]的和；同理T[8]储存的是A[1]到A[8]的和。

利用这个方法，如果想知道A[1]-A[7]的和，那么我们只需要知道T[7] , T[6] , T[4]即可，因为他们分别储存了A[7] , A[6]-A[5] , A[4]-A[1]的和。注意， 7(0111) 拆掉最后一个1之后为6(0110)，再拆掉最后一个1为4(0100)，再拆就为0(0000)了。

可以发现，如果我们想知道A的前缀和sum[k]，那么我们只需要将这个k每次拆掉最后一个1，然后在树状数组中去寻找T[k]累加即可。时间复杂度为 O(log n) 。

如果想要修改某个数字，那么我们只需要知道哪些节点储存了当前节点的值即可。观察上图，反过来加即可。

lowbit

那么就涉及到一个问题，怎么才能快速的把7拆开呢。那么就要引入 lowbit函数 ， lowbit函数 的产生其实与树状数组没有太大的关系，但是他可以高效的解决树状数组的问题。

int lowbit(int x){
    return x & (-x);
}

如果要理解 lowbit ，那么需要先知道数字是怎么用二进制来存储的。正数不用说，重要的是负数。

负数在计算机中是用补码来储存的，补码为正数所对应的二进制 取反后加一 。

例如-1，他是由1(0001)取反后(1110)加一(1111)。所以-1在二进制中存储为(1111)。-6在二进制中储存为(1010)，6在二进制中储存为(0110)，他们只有 最后一个1及后面所有的0是相同的 ，然后再取 与 ，就得到了 最后一个1及后面所有的0 。然后就可以将数字拆分了。

int query(int k){
    int sum = 0;
    for(int i = k;i;i -= lowbit(i)){
        sum+=T[i];
    }
    return sum;
}

区间查询

如上个例子所说，我们要查找前7个数的和，sum[7] = T[7] + T[6] + T[4]。而且我们可以发现 6 = 7 - lowbit(7) ， 4 = 6 - lowbit(6)，而且4 - lowbit(4)刚好等于0，就可以作为循环结束，于是我们只需要一个循环依次来减去他的 lowbit 即可得到拆分后的序列，然后相加即可。妙哉妙哉！

int add(int x){
    int sum = 0;
    for(int i = x;i;i -= lowbit(i)){
        sum += T[i];
    }
    return sum;
}

如果说对于某个区间的求和，利用前缀和的思想，对左节点和右节点依次求和，然后相减，over。

int add(int l, int r){
    int sum1 = 0;
    int sum2 = 0;
    for(int i = l-1;i;i -= lowbit(i)){
        sum1 += T[i];
    }
    for(int i = r;i;i = lowbit(i)){
        sum2 += T[i];
    }
    return sum2 - sum1;
}

单点修改

对于某个数字要修改的话，我们需要找到其父亲节点一起修改。

还是用这个图，如果我们要修改A[3]的值，那么T[3]，T[4]，T[8]都要修改。那么怎么从3得到4和8呢，万能的lowbit又登场辣。

仔细观察可以发现，4 = 3 + lowbit(3)， 8 = 4 + lowbit(4)，一直到超出范围再停止，妙蛙，一个循环又搞定了。

void change(int x, int k){
    for(int i = x;i <= n;i += lowbit(i)){
        T[i] += k;
    }
}

区间修改，单点查询

区间修改没法了，如果一个一个修改这就太麻烦了，那就买个挂吧，对于区间修改特别是多次的区间修改，最容易想到的就是差分。那么ok，那我们就创建一个差分的树状数组呗，这不就搞定了吗。

void update(int pos, int k){
    for(int i = pos;i <= n;i+=lowbit(i)){
        c[i] += k;
    }
}
update(l, k);
update(r+1, -k);

然后再对差分数组求和就可以得到答案了，差分数组的特点嘛。

int add(int pos){
    int sum = 0;
    for(int i = pos; i; i-= lowbit(i)){
        sum += c[i];
    }
}

区间修改，区间查询

A为原数组，D为差分数组

$\sum\limits_{i=1}^n A[i] = \sum\limits_{i=1}^n \sum\limits_{j=1}^i D[j]$

$=\sum\limits_{i=1}^n (n+1-i)\times D[i]$

$=\left[n\sum\limits_{i=1}^n D[i]\right]-\left[\sum\limits_{i=1}^n (i-1)D[i]\right]$

维护两个树状数组，sum1[i] = D[i]，sum2[i] = D[i]*(i-1);

struct BIT
{
    int n;
    ll a[N],b[N];
    int lowbit(int x)
    {
        return x&(-x);
    }
    void init(int n)
    {
        this->n=n;
        memset(a,0,sizeof(ll)*(n+1));
        memset(b,0,sizeof(ll)*(n+1));
    }
    void update(int pos,int val)
    {
        int x=pos;
        for(;pos<=n;pos+=lowbit(pos))
        {
            a[pos]+=val;
            b[pos]+=val*(x-1);
        }
    }
    void update(int l,int r,int val)
    {
        update(l,val);
        update(r+1,-val);
    }
    ll query(int pos)
    {
        int x=pos;
        ll res=0;
        for(;pos>0;pos-=lowbit(pos))
            res+=x*a[pos]-b[pos];
        return res;
    }
    ll query(int l,int r)
    {
        return query(r)-query(l-1);
    }
}bit;
bit.init();
for(int i=1;i<=n;++i)
    bit.update(i,a[i] - a[i-1]);
bit.update(l,r,k);
bit.query(l,r);

初始化树状数组

初始化看成n次修改

for(int i = 1;i <= n;i++){
    cin>>a[i];
    change(i, a[i]);
}

特别地，对于可以前缀和的信息，可以 $O(n)$ 初始化

void init()
{
    for (int i = 1; i <= n; ++i)
        t[i] = presum[i] - presum[i - lowbit(i)];
}

二维树状数组

struct BIT
{
    int n,m;
    int sum[N][N];
    int lowbit(int x)
    {
        return x & (-x);
    }
    void init(int nn,int mm)
    {
        n=nn;
        m=mm;
        for (int i = 1; i <= n; ++i)
            for (int j = 1; j <= m; ++j)
                sum[i][j] = 0;
    }
    void update(int x, int y, int val)
    {
        int tmp = y;
        for (; x <= n; x += lowbit(x))
            for (y = tmp; y <= m; y += lowbit(y))
                sum[x][y] += val;
    }
    int query(int x, int y)
    {
        int res = 0, tmp = y;
        for (; x > 0; x -= lowbit(x))
            for (y = tmp; y > 0; y -= lowbit(y))
                res += sum[x][y];
        return res;
    }
    int query(int x1, int y1, int x2, int y2)
    {
        return query(x2, y2) - query(x1 - 1, y2) - query(x2, y1 - 1) + query(x1 - 1, y1 - 1);
    }
} bit;

权值树状数组，单点修改，全局第k小

类似权值线段树，维护值域

当前缀值域小于k，那么前面都不是第k小

int kth(int k)
{
    int sum = 0, x = 0;
    for (int i = __lg(n);i>=0; --i)
    {
        x += 1 << i;
        if (x >= n || sum + t[x] >= k)
            x -= 1 << i;
        else
            sum += t[x];
    }
    return x + 1;
}