二项式反演

约 353 个字 预计阅读时间 1 分钟

解决“多个条件恰好满足几个“这类计数问题。

恰好不好求，因为不仅需要 $i$ 个满足，而且需要 $n−i$ 个不满足

形式1

$g(i)$ 表示 $n$ 个条件，恰好满足 $i$ 个的情况数，的总和

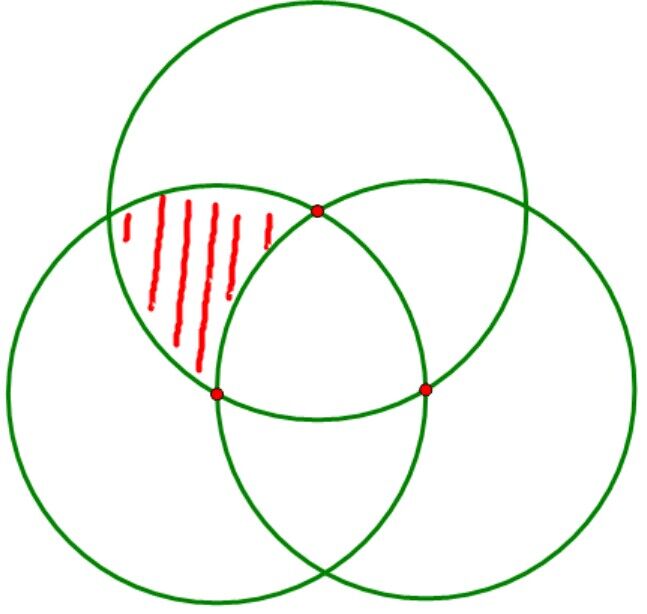
以下的图 $n=3$,

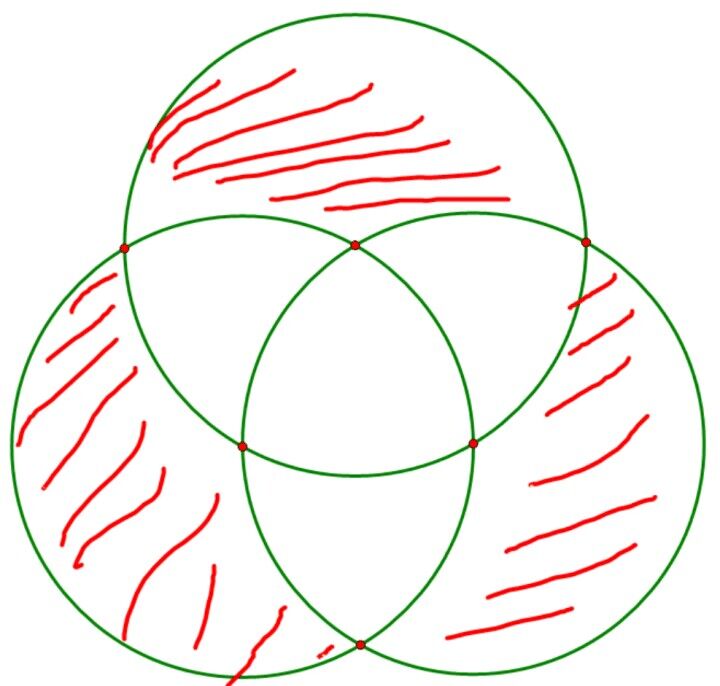
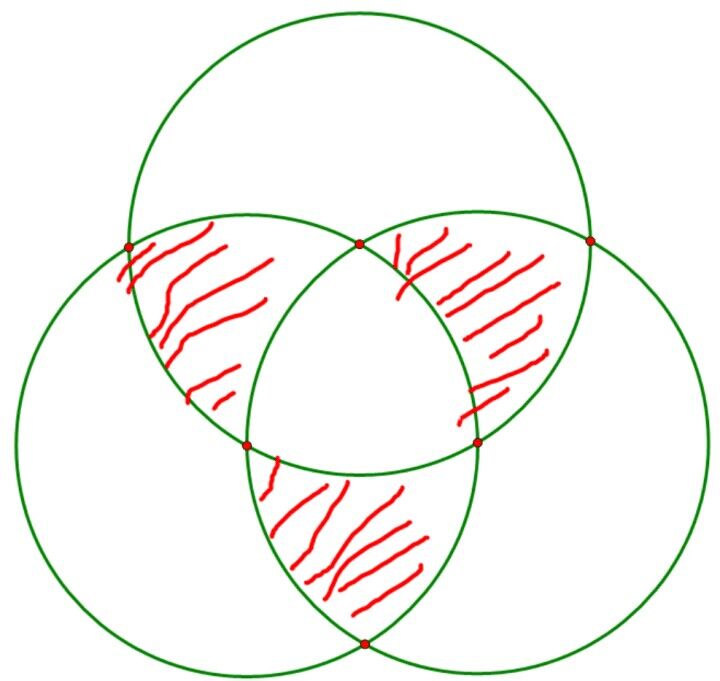
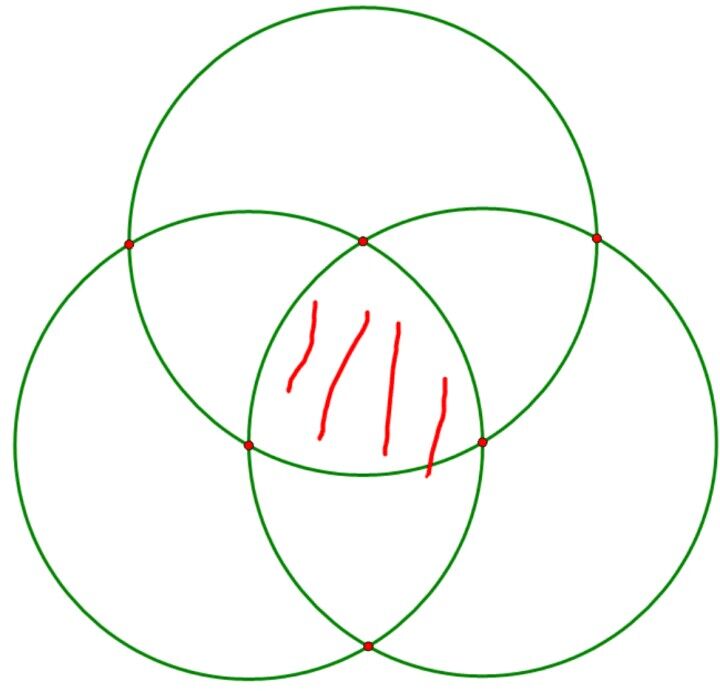
$f(k)$ 表示选择 $k$ 个满足，剩下 $n−k$ 个随意的情况数，的总和

$f(1)=$ 三个圆形面积的和 $=g(1)+2g(2)+3g(3)$

通常情况是 $f$ 可以DP算出来，然后通过以下公式反演出 $g$

$f(k)=\sum\limits_{i=k}^n \dbinom ik g(i)$

$g(k)=\sum\limits_{i=k}^n (-1)^{i-k}\dbinom ikf(i)$

形式2

$g(i)$ 表示 $n$ 个条件，恰好满足 $i$ 个的情况数，但不是总和

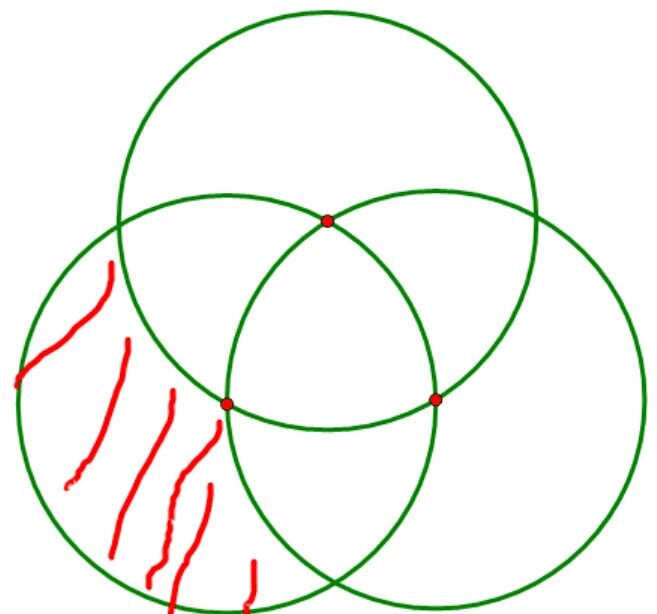
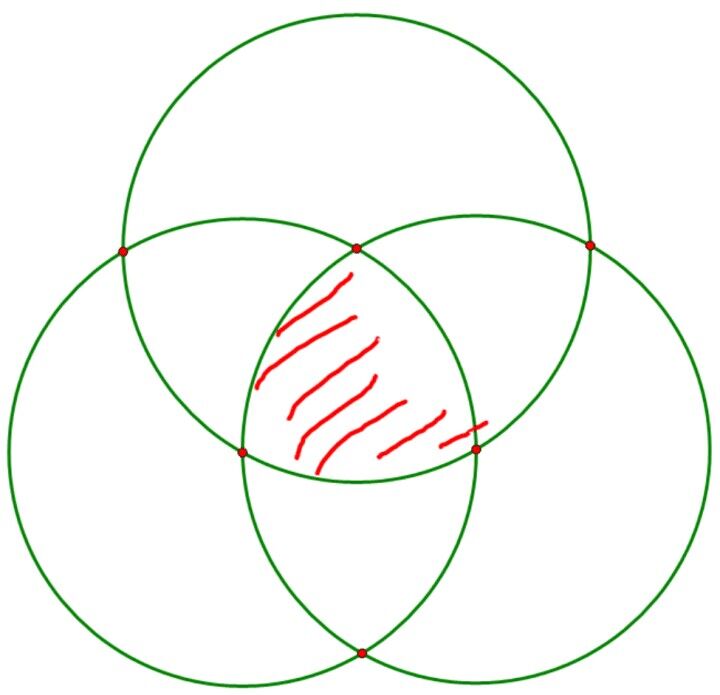
$f(k)$ 表示选择 $k$ 个满足，剩下 $n−k$ 个随意的情况数，但不是总和

$f(3)=$ 三个圆形面积的并 $=3g(1)+3g(2)+g(3)$

通常情况是 $f$ 可以组合数学或者DP算出来，然后通过以下公式反演出 $g$

$f(k)=\sum\limits_{i=m}^{k} \dbinom ki g(i)$

$g(k)=\sum\limits_{i=m}^k (-1)^{k-i}\dbinom kif(i)$

个人感觉对满足条件个数相同，条件序号选择不同，g(i)相等时用形式2，否则用形式1

比如g(1)选左下还是上面还是右下的数量都一样，那么用形式2

例题

形式2：

luogu p5505

形式1：

luogu p4859

luogu p6478